Programmable Logic Controller (PLC) အေၾကာင္း အေျခခံ ေလ့လာသင္ယူခ်က္ - ၃

Programmable Logic Controllers Chapter 2 - Number System and Codes

Programmable Logic Controllers
Chapter 2 - Number System and Codes
PLC မ်ားကုိ ကၽြမ္းက်င္စြာအသံုးခ်ႏုိင္ရန္ number system မ်ားႏွင့္ Digital codes မ်ားအေၾကာင္းကို အေၿခခံမွစ၍ စနစ္တက် နားလည္ရန္လုိအပ္သည္။ Input/Output တုိ႔၏ address မ်ား သတ္မွတ္ေပးရန္ႏွင့္ programming လုပ္ရန္အတြက္ Number system ၄ မ်ိဳးကုိ ပထမဦးစြာရွင္းလင္း ေဖာ္ၿပထားသည္။

(က)Binary System
(ခ) Octal System
(ဂ) Decimal System ႏွင့္
(ဃ) Hexadecimal System တို႔ျဖစ္သည္။

Binary Coded Decimal (BCD) ႏွင့္ Gray codes မ်ားႏွင့္အတူ ASCII character set ႏွင့္ PLC register format မ်ားအေၾကာင္းကုိ ရွင္းလင္းေရးသားထားသည္။ Number System မ်ားသည္ PLC logic မ်ား၏ အေျခခံ အုတ္ျမစ္မ်ားျဖစ္သည္။ ဤ code မ်ားကုိနားလည္ႏွံစပ္ျခင္းျဖင့္ PLC မ်ားအ အလုပ္လုပ္ပံုကုိ ေကာင္းစြာသိျမင္နားလည္ႏုိင္သည္။

၂.၁ Number System
Number System မ်ားကုိ ကြ်မ္းက်င္ ပုိင္ႏုိင္လွ်င္ PLC မ်ားကိုမိမိလုိသလုိ ေကာင္းစြာအသံုးခ်နုိင္သည္။ အေျခခံက်ေသာ (Basic) function မ်ားမွာ Number မ်ားျဖင့္ ေဖာ္ျပျခင္း (representation) , Number မ်ားကုိ သိမ္းဆည္းျခင္း (Store) ႏွင့္ Number မ်ားကုိ ေပါင္းႏႈတ္ေျမွာက္စား စသည့္ Operation မ်ားၿပဳလုပ္ျခင္းတုိ႔ျဖစ္သည္။ PLC မ်ားသည္ Binary Number မ်ားကိုအသံုးၿပဳ၍တန္ဘုိးမ်ားကိုေဖာ္ၿပၿခင္း၊ သိမ္းဆည္းၿခင္း တုိ့ၿပဳလုပ္သည္။

မည္သည့္ Number System ပင္ျဖစ္ပါေစေအာက္ပါအခ်က္မ်ားအားလုံးအက်ဳံးဝင္သည္။သက္ဆိုင္ သည္။

(က) Number System အားလံုးတြင္ Base တန္ဘုိး တစ္မ်ိဳးမ်ိဳးကို အေၿခခံ၍တည္ေဆာက္ထားသည္။
(ခ) Number System အားလံုးကို ေရတြက္ရာတြင္ (Counting လုပ္ၿခင္း) အသံုးၿပဳႏိုင္သည္။
(ဂ) Number System အားလံုးကို တန္ဘုိးမ်ား ၊ ပမာဏမ်ား(quantities)ႏွင့္ code မ်ားကို ေဖာ္ၿပရန္ အသံုးၿပဳသည္။
(ဃ) Number System အားလံုးတြင္ သေကၤတမ်ား (set of symbol) ရွိၾကသည္။

Number System တစ္ခု၏ Base သည္ ထုိ System က အသုံးျပဳသည့္ unique symbol ျဖစ္သည္။ အျမင့္ဆုံး (အမ်ားဆုံး) တန္ဘုိးသည္ Base ထက္ ၁ ေလ်ာ့သည္။ ၂ ကုိ အေျခခံ၍ တည္ေဆာက္ထားေသာ Number System ကုိ Base 2 ဟုေခၚဆုိသည္။ မည္သည့္ တန္ဘိုးကုိမဆုိ Base အျဖစ္တည္ေဆာက္ႏုိင္ေသာ္လည္း ၊ PLC မ်ားတြင္အသုံးမ်ားေသာ Number System မ်ားမွာ Base 2 ၊ Base 8 ၊ Base 10 ႏွင့္ Base 16 တုိ႔ျဖစ္ သည္။

Base 2 System ကုိ Binary System ဟုလည္းေကာင္း၊
Base 8 System ကုိ Octal System ဟု လည္းေကာင္း၊
Base 10 System ကုိ Decimal System ဟု၍ လည္းေကာင္း၊
Base 16 number System ကုိ Hexadecimal number System ဟူ၍၎ ေခၚဆုိသည္။

ထုိ System မ်ားအားလုံးကုိ နားလည္ရန္ ပထမဦးဆုံး ရင္းႏွီးနားလည္ၿပီးသားျဖစ္သည့္ Decimal System မွစတင္ရေအာင္…

၂.၂ Decimal System
Decimal System ကုိ ကၽြႏု္ပ္တုိ႔အားလုံး နားလည္ၿပီးျဖစ္သည္။ လူမ်ားတြင္လက္ေခ်ာင္းက ေလးမ်ား ၁၀ ေခ်ာင္း၊ ေျခေခ်ာင္းကေလးမ်ား ၁၀ ေခ်ာင္းစီရိွၾကေသာေၾကာင့္ Decimal Number System ႏွင့္အလြန္ရင္းႏွီး ကြ်မ္းဝင္ၿခင္း ျဖစ္သည္။ Decimal Number System သည္ ၁၀ ကုိအေျခခံထားသည့္ Base 10 System ျဖစ္သည္။ 0,1,2,3,4,5,6,7,8 ႏွင့္ 9 တုိ႔ကို Symbol မ်ား သုိ႔ မဟုတ္ Digits မ်ားဟုေခၚဆုိသည္။

ထုိ႔ေၾကာင့္ System symbol အားလုံးစုစုေပါင္း 10 ခုရိွသည္။ ( ဝ မွ ၉ အထိ) အ ျမင့္ဆုံးတန္ဘုိး 9 သည္ Base ျဖစ္သည့္ 10 ထက္ ၁ ေလ်ာ့ေနသည္။ Decimal System မ်ားသည္ အလြန္ ရင္းႏွီးလြန္းေသာေၾကာင့္ အျမင့္ဆုံးတန္ဘိုးျဖစ္သည္ 9 ထက္မ်ားပါ မည္ကဲ့သုိ႔ေဖာ္ျပရမည္ကုိ စဥ္းစားမိရန္ခဲယဥ္းသည္။ အျမင့္ဆုံးဂဏန္း (Largest Symbol) ထက္ပုိမ်ားသည့္တန္ဘိုးကုိေဖာ္ျပသည့္နည္းမ်ားသည္ Number System အားလုံးတြင္တူညီၾကသည္။
Decimal System တြင္ ပါဝင္သည့္ဂဏန္းမ်ားတန္ဘုိးသည္ ေနရာကုိလုိက္၍ ေျပာင္းလဲသည္။ Place Value သုိ႔မဟုတ္ weight ဟုေခၚသည္။ ညာဘက္မွ ဘယ္ဘက္သုိ႔ (from right to Left ) သုိ႔ ေရာက္သြားေလေလ တန္ဘုိးမ်ားေလေလျဖစ္သည္။
ပုံ2-1 တြင္ေဖာ္ျပထားသည္။ ညာဘက္အစြန္ဆုံး (right most) ေနရာ၏ position တန္ဘိုး သည္ ၀ (သုည) ျဖစ္သည္။ အကယ္၍ Base 10 (သုိ႔) Decimal ျဖစ္ခဲ့လွ်င္ ပုံ ၂-၂ တြင္ position (ေနရာ) မ်ားအားလုံး ၏ weight value ကုိ 10 ကုိ အေျခခံ၍ေဖာ္ျပထားသည္။ Decimal System အတြက္ ညာဘက္မွ ဘယ္ဘက္ သို႔ (from right to left) position weight မ်ားမွာ ၁ ၊ ၁၀ ၊ ၁၀၀ ၊ ၁၀၀၀ စသည္တုိ႔ျဖစ္သည္။ ထုိကဲ့သို႔ တန္ ဘုိုးမ်ားကုိ ေရတြက္သည္နည္းကုိ “Sum of the Weight Method” ဟုေခၚသည္။

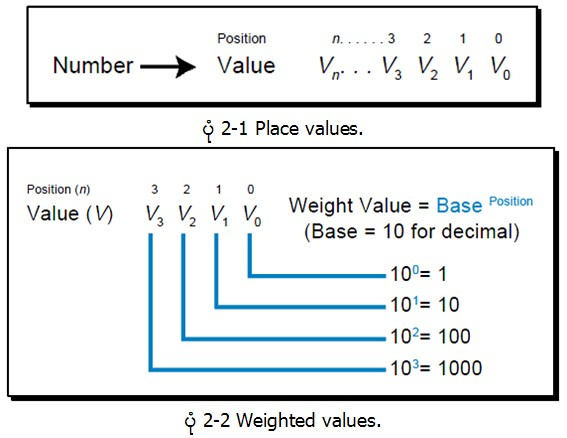
Decimal number မ်ား၏တန္ဘုိးကုိရရန္ Digit ႏွင့္ေနရာ၏တန္ဘိုး (Weight value) တုိ႔ကုိ ေျမွာက္ၿပီး တန္ဘုိးမ်ားအားလုံးကုိေပါင္းယူျခင္းျဖစ္သည္။ ဥပမာ-အေနျဖင့္ 9876 ကုိ “Sum of the Weight Method” method ျဖင့္ ေအာက္ပါအတုိင္းတြက္ယူႏုိင္သည္။

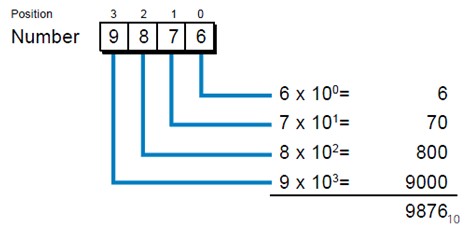
ဂဏန္းတုိင္း (Digit တုိင္း) ကုိ Base ကုိမူတည္၍ ေနရာ၏ ထပ္ကိန္းတန္ဘုိးရွာယူျခင္းျဖစ္ သည္။ထုိ႔ေၾကာင့္ No မွ Nn အထိေပါင္းလွ်င္ Base “b” ျဖစ္ေသာ Decimal equipment တန္ဘိုးကုိရသည္။

၂-၃ Binary Number System
Binary number System သည္ ၂ ကုိအေျခခံ၍ တည္ေဆာက္ထားေသာ (Base 2) စနစ္ျဖစ္သည္။ ထုိ႔ ေၾကာင့္ Binary Number System တြင္ရိွ 0 ႏွင့္ 1 သာရိွႏုိင္သည္။ ၂ ၊ ၃ ၊ ၄ စသည့္ ဂဏန္းမ်ားမပါဝင္ႏုိင္ေပ၊ PLC ႏွင့္ Digital Computer မ်ားကဲ့သုိ႔ေသာ Device မ်ားအတြက္ Binary Number System သည္အသုံးအဝင္ဆုံးျဖစ္သည္။ Binary Number System ကုိသာသုံး၍ Operation လုပ္ႏုိင္သည္။ 0 ႏွင့္ 1 ႏွစ္မ်ိဳးကုိသာ အေျခခံ၍ ဒီဇုိင္းလုပ္ထားေသာေၾကာင့္ Device မ်ားအတြက္ Operate လုပ္ရန္ လြယ္ကူသည္။ မီး လုံး ၊ ဘား (value) ႏွင့္ ခလုပ္ (switch) စသည့္ physical element မ်ားတြင္ ON/OFF , Close/Open ႏွင့္ Start/Stop စသည္ အေျခအေန (state) ၂ မ်ိဳးသာရိွႏုိင္သည္။
Computer ကုိအသုံးျပဳသည့္အခါတုိင္း Binary Number System ကုိ ေတြ႔ျမင္ႏုိင္သည္။ Computer ကုိသုံးလုိလွ်င္ ခလုပ္ကုိဖြင့္ (ON) လုိက္သည့္ႏွင္တစ္ၿပိဳင္နက္ ခလုပ္သည္ Position “0” မွ Position “1” အျဖစ္သိ႔ုေျပာင္းသြားသည္။ Computer ကုိ အသုံးမျပဳေတာ့လွ်င္ Position “0” သုိ႔ျပန္ေရာက္ေစၿပီး ပိတ္ (OFF) ပစ္လုိက္သည္။ Digital circuit မ်ားတြင္ Voltage ၂ မ်ိဳးျဖင့္ခဲြျခားထားသည္ +5 V ႏွင့္ 0 V ျဖစ္သည္။ ထုိ႔ေၾကာင့္ Digital application မ်ားအတြက္ Binary number System သည္အလြန္အသုံးဝင္သည္။ Binary Number System တြင္ 1 သည္ အၾကီးဆံုးတန္ဘုိး( largest valued System) ျဖစ္သည္။

Decimal System မ်ားမွာကဲ့သုိ႔ပင္ Binary Number System တြင္ Largest valued System ထက္ႀကီးသည့္တန္ဘုိးကုိ ေဖာ္ျပလုိလွ်င္ ညာဘက္မွ ဘယ္ ဘက္သို႔ (From Right To Left) ေနရာတစ္ေနရာေရြ႕၍ weighted value ကုိ assign လုပ္ျခင္းျဖစ္သည္။ Weight Value (Decimal equipment) မ်ား တြက္ပုံမွာ Decimal Number System ႏွင့္ Binary Number System တုိ႔တြင္တူညီသည္။ ကဲြျပားသည့္အခ်က္မွာ Decimal Number System တြင္ Base ျဖစ္သည့္ ၁၀ ၏ အေပၚ၌ ထပ္ကိန္းတင္ျခင္းျဖစ္ၿပီး၊ Binary Number System ၌ Base ျဖစ္သည့္ ၂ အေပၚတြင္ထပ္ကိန္းတင္ ျခင္းျဖစ္သည္။ ထပ္ကိန္းသည္ position ၏ ေနရာပင္ျဖစ္သည္။ Binary Number System တြင္ ညာမွဘယ္သုိ႔ (From Right To Left) ေရႊ႕သြားသည္ weight value မွာ 1,2, 4, 16, 32, 64 စသည္တုိ႔ျဖစ္ၿပီး ေနရာ 0,1,2,3,4,5,6 တုိ႔ျဖစ္သည္။

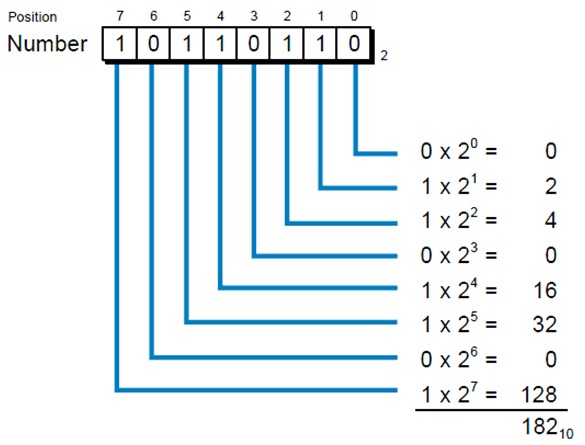
ဥပမာ-အေနျဖင့္ Binary Number 10110110 ႏွင့္ တန္ဘိုးတူညီသည့္ Decimal value ကုိ တြက္ၾကရေအာင္၊

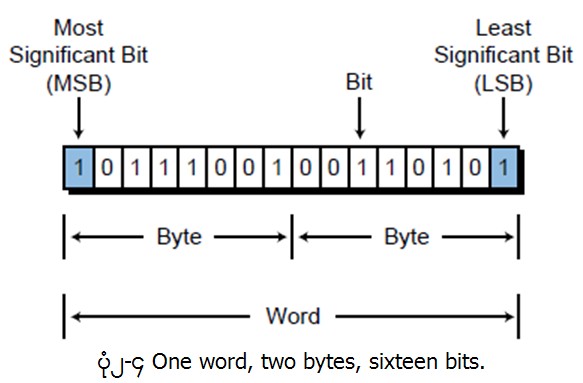
Binary number 10110110 သည္ Decimal Number System မွ 182 ႏွင့္ တန္ဘုိးတူညီသည္။ Binary number ၈ လုံး (8 digit) ကုိ bit တစ္ခုအျဖစ္သတ္မွတ္သည္။ Binary Number 10110110 (182 decimal ) သည္ 8bit ရိွသည္။ bit ၈ ခုရိွသည္။ bit ၄ ခုရိွလွ်င္ Nibble ဟုသတ္မွတ္သည္။ bit ၈ ခုရိွလွ်င္ byte တစ္ခုအျဖစ္သတ္မွတ္သည္။ ၁ ခု ထက္ပိုမ်ားသည့္ byte မ်ားကုိ “word” အျဖစ္သတ္မွတ္သည္။ ပုံ၂-၄ တြင္ bit ၁၆ ခုရိွသည့္ Binary Number ကုိေဖာ္ျပထား သည္။
ဘယ္ဘက္အစြန္ဆုံး၌ရိွသည့္ ဂဏန္း (Digit) မွာ Least Significant bit (Lowest valued bit) ျဖစ္သည္။ ညာဘက္အစြန္ဆုံး၌ရိွသည့္ ဂဏန္း (Digit) မွ Most Significant bit (MSB) ျဖစ္ၿပီး အမ်ားဆုံး တန္ဘိုးရိွသည့္ bit (Most significant bit) ျဖစ္သည္။

Binary Number မ်ားကုိေရတြက္ရန္ အလြန္ခြတိခြက်ႏုိင္ျခင္းမွာ Binary Number မ်ားကုိ Decimal Number မ်ားကဲ့သုိ႔မရင္းႏွီးေသာ ေၾကာင့္ ျဖစ္သည္။ Binary Number System ႏွင့္ 0 ႏွင့္ 1, ၁ ၿပီးေနာက္ေနရာတစ္ေနရာေရႊ႕ၿပီးျပန္ျဖစ္သည္။ Decimal Number တြင္ ၁ မွ ၉ ၊ ၉ၿပီး ေနာက္ေနရာေရႊ႕ၿပီး ၁ ျပန္ျဖစ္သည္။

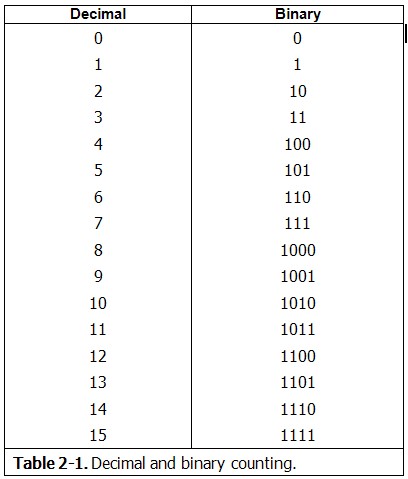
Table 2-1 တြင္ Binary Number ႏွင့္ Decimal Number တုိ႔ကုိ ယွဥ္၍ေဖာ္ျပထားသည္။
၂.၄ Octal Number System
Binary Number System တြင္ Digit မ်ားစြာပါရိွရန္လုိသည္။ Decimal Number ထက္ပုိ၍မ်ားသည္။ ဥပမာ- Decimal Number မွ 9110 သည္ Binary Number 10110112 ႏွင့္ညီသည္။ Digit မ်ားကုိေရးရန္၊ ဖတ္ရန္ အလြန္ခက္ခဲသည္။ အထူးသျဖင့္ လူမ်ားဖတ္ယူရန္ အတြက္ပုိ၍ အဆင္မေျပေပ။
ထုိ႔ေၾကာင့္ အလြန္ Digit မ်ားသည့္ Binary Number မ်ားကုိ ေဖာ္ျပရန္အတြက္ Octal Number System ကုိအသုံးျပဳေလ့ရိွ သည္။ Octal Number System သည္ ၈ ကုိအေျခခံထားသည့္ Base 8 စနစ္ျဖစ္သည္။ Digit ၈ လုံးသာပါဝင္သည္။ 0,1,2,3,4,5,6 ႏွင့္ 7 တုိ႔ျဖစ္သည္။ Table 2-2 တြင္ ၁ မွ ၁၅ အထိကုိ Decimal ၊ Binary ႏွင့္ Octal တုိ႔ျဖင့္ ယွဥ္ တဲြေဖာ္ျပထားသည္။

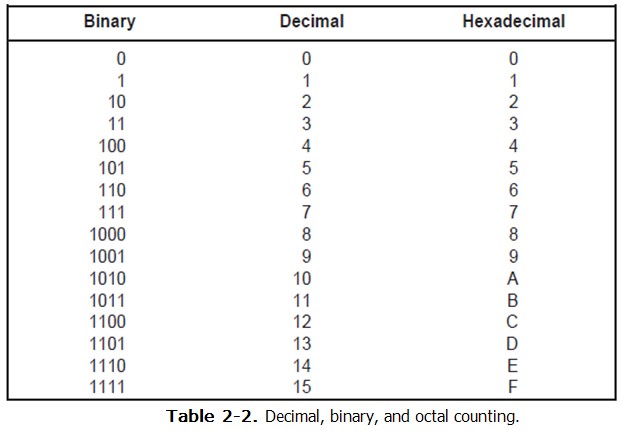
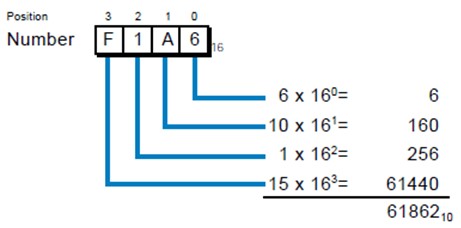
ျခားေသာ Number System မ်ားကဲ့သို႔ပင္ Octal Number တြင္ေနရာ (position ) တန္ဘုိးကုိ weighted ျဖင့္ေဖာ္ျပ သည္ ။ ဥပမာ- Octal Number 1767 ႏွင့္ တန္ဘုိးတူညီသည့္ Decimal Number မွာ 1015 ျဖစ္သည္။

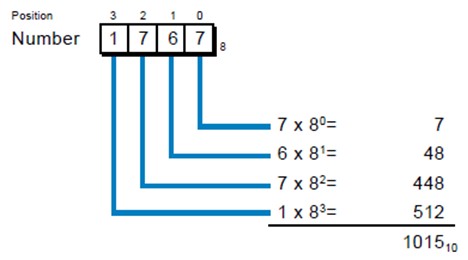
ေအာက္တြင္ 16-bit ရွိသည့္ binary number ကို six digits သာ octal number ၿဖင့္ေဖာ္ၿပထားသည္။

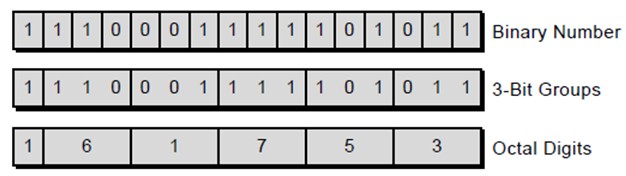
Octal Number သည္ Binary Number မ်ားကုိပုိ၍ အဆင္ေျပစြာ ေဖာ္ျပႏုိင္ရန္အတြက္ သုံးျခင္းျဖစ္သည္။ Binary Number ရိွ Digit ၃ ခု( binary bit 3) ကုိ တစ္ခုခုလုိက္ၿပီး Octal Number တစ္လုံး (Digit 1 ခု) အျဖစ္ေဖာ္ျပႏုိင္သည္။ ထို႔ေၾကာင့္ အလြန္ မ်ားျပားသည့္ (ရွည္လ်ားသည့္) Binary Number မ်ားကုိ ON ကုိသုံး၍ Digit အနည္းငယ္ျဖင့္ ေဖာ္ျပႏုိင္သည္။ ဥပမာ- 16bit Binary Number ကုိ Octal Number ျဖင့္ေဖာ္ျပလွ်င္ ဂဏန္း ၆လုံး ( 6 Digits) သာလုိသည္။ PLC မ်ားတြင္ input/output address မ်ား ႏွင့္ memory address မ်ားကုိေဖာ္ျပရန္အတြက္ Octal Number ကုိအသုံးျပဳၾကသည္။

ေကာင္းထက္ညြန့္